Komentovaný přehled mnohorozměrných statistických metod používaných v ekologii

Komentovaný přehled mnohorozměrných statistických metod používaných v ekologii

Karel Matějka

Příspěvek byl přednesen na semináři "Problematika lesnické typologie IV" uspořádaném Lesnickou fakultou ČZU Praha-Suchdol v Kostelci nad Černými lesy 30. a 31. lesna 2002.

Úvod

Mnohorozměrné matematicko statistické metody se v současnosti již široce používají v mnoha oblastech biologie a ekologie. Stejně uplatnitelné jsou i v lesnické typologii, která poskytuje data svým charakterem odpovídající jiným datům - zvláště snímkům klasické fytocenologie. Předkládaný příspěvek by měl ukázat některé aspekty charakteru a použití těchto metod - to bez nároku na úplnost předkládaných informací, a vzhledem na charakter článku i na kompletní autorskou originálnost. Mnoho předložených thesí již bylo publikováno a něcoje i dostatečně známo např. v biomatematických kruzích.

Za mnohorozměrné matematicko statistické metody jsou považovány ty, kde jsou zpracovávána data vzniklá jako realizace vícerozměrného náhodného procesu - jednoduše řečeno, při jednom měření nebo na jednom vzorku získáváme řadu jednoduchých údajů, které nám popisují stav šetřeného objektu a takto získaná data dále zpracováváme. Klasickým případem se nám může stát šetření na lokalitě, kde zjišťujeme například složení vegetace (výskyt každého druhu rostlin představuje jednu proměnnou) a/nebo řadu půdních vlastností. Dalších příkladů a jejich modifikací je možné najít vlastně neomezeně.

Prvním úkolem po získání dat je jejich logické uložení do nějakého strukturovaného datového souboru, včetně potřebného kódování dat. Přitom je potřebné vycházet z reálně předpokládané (nebo známé) vazby mezi jednotlivými proměnnými a z požadavků na možné dotazování v datech. Tyto otázky jsou řešeny v rámci problematiky databází a “data warehousing”, což jsou dnes do značné míry samostatně rozvíjené obory.

Druhým krokem je hledání odpovědí na základní otázku "Jaké jsou skryté informace v datech?" Oblast zpracování dat řešící tuto problematiku bývá nazývána "data mining". Zde bývají uplatňovány nejrůznější postupy - například neuronové sítě nebo metoda GUHA (Hájek et al., 1983). Sem lze zařadit rovněž matematicko statistické postupy zpracování dat a v prvé řadě i mnohorozměrné metody.

Tyto metody vycházejí z pravděpodobnostních a statistických základů, někdy však stránka statistické interpretace bývá potlačena - statistické testování tak nemusí být prvořadým cílem. Tím se potom stává “Exploratory data analysis”. Původní základ však nesmí být přehlížen, protože v opačném případě by mohlo docházet k chybné interpretaci výsledků.

Členění mnohorozměrných statistických metod

Mezi mnohorozměrné metody lze řadit například

Mnohorozměné korelace - korelační analýza dává většinou základní přehled o hodnocených datech, mnohdy je i základem pro další metody.
Stepwise regression (linear, nonlinear) - Při této regresní metodě se snažíme o popis maximální variability v datech na základě minimálního počtu "vysvětlujících" proměnných. V rozsáhlejších datových souborech však tento postup může být i nepřehledný. Užitečný je např. pro ověření předchozích znalostí nebo hypothes.
MANOVA - mnohorozměrná obdoba analýzy variance
Discriminant analysis - metoda, která se snaží najít takové funkce více proměnných, na základě nichž lze rozlišit vozorky (realizace mnohorozměrného náhodného procesu) do dvou nebo více definovaných skupin.

Do skupiny mnohorozměrných metod mimo další pak náleží i dvě zvláště významné skupiny postupů - klasifikace a ordinace.

Klasifikační metody

Členění metod

Hierarchické

Aglomerativní
Divisivní

Nehierarchické

Metody zachovávající počet shluků (“K-means”): Forgyova metoda, Jenceyova metoda, MacQueenova metoda, Wishartova metoda
Metody s proměnným počtem shluků

Dále je možné mezi klasifikační metody zařadit

Two-way joining - postupy pro společnou klasifikaci vzorků i atributů; používají se zvláště pro uspořádání fytocenologických tabulek.
a jiné metody (fuzzy klasifikace, ...)

Popis metod

Existuje řada publikací, kde je možné najít popis používaných klasifikačních metod. V češtině to byla například publikace Lukasová et Šarmanová (1985). Dále je vhodné upozornit například na na dnes již klasické publikace Whittaker (1973), van der Maarel (1980) nebo Legendre et Legendre (1983).

Porovnání klasifikačních metod

Pro porovnání byla použita data fytocenologických snímků z bukových porostů Orlických hor (17 ploch snímkovaných opakovaně mezi lety 1951 a 2001; data S. Vacek, VÚLHM Výzkumná stanice Opočno, viz Matějka, 2001).

Počítány byly následující klasifikace podle složení bylinného patra

Nearest neighbour method: Euclidean distance (chaining 49,14%; Obr. 1)
Farthest neighbour method: Euclidean distance (chaining 7,10%; Obr. 2)
Ward’s method: squared Euclidean distance (chaining 5,08%; Obr. 3)
Group average: Sörensen’s similarity (chaining 18,04%; Obr. 4)

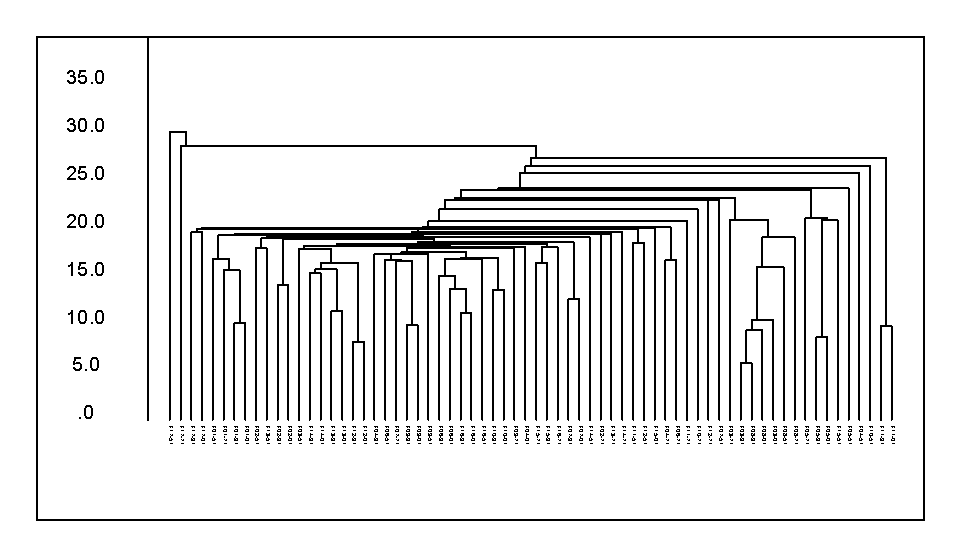
Porovnání klasifikačních metod je možné provést na základě grafů vývoje shlukování - viz Obr. 5 a 6. Zde je rovněž patrný rozdílný podíl řetězení vzorků u jednotlivých metod.

Divisivní klasifikační metody

Klasickou metodou je procedura TWINSPAN (Hill, 1979).

Klasifikace uspořádaných vzorků

Pro uspořádané vzorky bylo vyvinuto několik postupů, které shlukují vzorky podle jejich předem zadaného pořadí (případně uspořádání ve vícerozměrném prostoru) - viz Gordon (1973), Legendre (1987) nebo Matějka (1993).

Uspořádání vzorků může být podle rozložení vzorků v geografickém prostoru (lineární - podél transektu nebo dvourozměrné - v ploše krajiny). Další možností je uspořádání podle jedné nebo více os proměnných prostředí.

Další poznámky ke klasifikačním metodám

Vliv transformace dat je možné ukázat výhodným způsobem při použití klasifikace uspořádaných vzorků - tak tomu je například u metody HSCA/Sq. Ve výsledném obraze jsou totiž vzorky stále ve stejném pořadí, čímž vynikne vliv požadovaného efektu.

V presentovaném příkladu to je mocninná transformace dat s použitými exponenty 0,1 až 2,511. První hodnota ukazuje výsledky blížící se klasifikaci snímků na základě dat presence/absence druhů, poslední nejvyšší hodnota klasifikuje snímky podle zjištěných dominantních druhů.

Data v tomto příkladě byla použita z transektu číslo 106 (z roku 1986) pořízeném podél gradientu bylinnou vegetací na opuštěných polích v oblasti Chelčic v jižních Čechách (Obr. 7).

Pomocí klasifikace uspořádaných vzorků lze hodnotit rovněž chování klasikačních metod vzhledem ke gradientům prostředí a ekotonů. Ekoton si tak můžeme představit jako takové místo na topografickém gradientu, kde se silně mění charakter prostředí. Vzorky z ekotonu mohou být klasifikovány jako samostatný shluk nebo mohou být přiřazovány ke dvěma sousedním shlukům (Obr. 8).

Ordinační metody

První skupina ordinačních metod je založena sledování vzdáleností mezi hodnocenými vzorky (Distance-based techniques) - sem náleží

Polar ordination (PO) [Bray-Curtis ordination]
Principal coordinates analysis (PCoA)
Nonmetric Multidimensional Scaling (NMDS)

Druhá, dnes snad významnější skupina metod pracuje s vlastními čísly a vektory matic podobností, korelačních nebo kovariačních matic (Eigenanalysis-based techniques). Zde byly rozlišeny postupy

nepřímé gradientové analýzy (Indirect gradient analysis), které se opírají pouze o složení hodnocených vzorků (fytocenologických snímků) - existují dva rozdílné přístupy k datům

Linear Model: Principal Components Analysis (PCA)
Unimodal Model (tento model předpokládá gaussovské rozložení výskytu druhů podél počítaných gradientů, jinými slovy - na gradientu existuje jeden bod optima pro výskyt každého druhu):

Correspondence Analysis (CA) [Reciprocal averaging]

Detrended Correspondence Analysis (DCA) (viz Hill and Gauch 1982)

Vztah mezi oběma metodami a jejich možnosti pro zobrazení gradientů prostředí jsou znázorněny na obr. 14

přímé gradientové analýzy (Direct gradient analysis), které již při vlastním výpočtu užívají externí informace o hodnocených vzorcích (v případě fytocenologických snímků se jedná o informace o prostředí)

Linear Model: Redundancy Analysis (RDA)
Unimodal Model:

Canonical Correspondence Analysis (CCA) (viz ter Braak, 1986)

obdobně jako u skupiny nepřímých ordinačních metod, i zde byla vyvinuta metodat detrended CCA (DCCA)

Příklady použití ordinačních metod pro hodnocení vývoje lesních porostů

Dříve uvedená data opakovaných fytocenologických snímků v bukových porostech Orlických hor byla použita jako příklad pro srovnání několika ordinačních metod:

Principal component analysis (ordinary PCA) (první čtyři vlastní čísla l ₁=0,3212, l ₂=0,1807, l ₃=0,1552, l ₄=0,0657; Obr. 9)
Correspondence analysis (CA) (vlastní čísla l ₁=0,5380, l ₂=0,3757, l ₃=0,2884, l ₄=0,2621; Obr. 10)
DCA: Detrending by segments (vlastní čísla l ₁=0,5380, l ₂=0,2976, l ₃=0,2031, l ₄=0,1652; Obr. 11)
DCA: Detrending by 2nd order polynomials (vlastní čísla l ₁=0,5380, l ₂=0,3396, l ₃=0,2486, l ₄=0,2143; Obr. 12)

Uveden je rovněž graf ordinace druhů, který byl konstruován na základě výsledků poslední uvedené ordinační metody (Obr. 13)

Typy PCA

Metoda hlavních komponent má různé varianty, které se liší úpravou dat před vlastním výpočtem. Přehled používaných možností je uveden v následující tabulce.

	Vektor vzorků	Vektor druhů	"Scaling"
"Ordinary"		centrován	Euclidean distance biplot
"Standardized"		3	Euclidean distance biplot
"duble centred"	centrován	centrován	symetrical scaling
"standardized by sample norm"	standardizován na jednotkovou normu		Euclidean distance biplot
"standardized by sample norm & centred by species"	standardizován na jednotkovou normu	centrován	Euclidean distance biplot
"centred and standardized by samples"	centrován a standardizován		Euclidean distance biplot
"noncentred"			Euclidean distance biplot / symetrical scaling
principal coordinates analysis (PCoA)	centrován	centrován	symetrical scaling

Porovnání NMDS a DCA

Computation time	High	*Low*
Distance metric	Highly sensitive to choice of distance metric	*Do not need to specify*
Simultaneous ordering of species and samples	No	Yes
Arch effect	Rarely occurs	Artificially and inelegantly removed
Related to direct gradient analysis methods	No	Yes
Need to pre-specify numbers of dimensions prior to interpretation	Yes	No
Need to specify parameters for number of segments, etc.	No	Yes
Solution changes depending upon number of axes viewed	Yes	No
Handles samples with high noise levels	No(?)	Yes
Guaranteed to reach the global solution	No	Yes
Results in measures of beta diversity	No	Yes
Used in other disciplines (e.g. psychometry)	Widely	(?)
Axes interpretable as gradients	No	Yes
Derived from a model of species response to gradients	No	Yes

Dalším příkladem použití ordinačních metod je hodnocení vztahu vegetace a půdy podél lučního transektu na pobřeží Kratochvílského rybníka, který byl složený z kvadrátů 1m². Porovnávat tak je možné například druhové složení vegetace a charakteristika humusových látek na základě výsledků dvou nezávislých ordinačních analýz (Obr. 15).

Závěrečné poznámky

Mezi metody, které jsou často používány nebo si zasluhují pozornost, je možné najít následující

Classification or Cluster Analysis: ADE-4, CAP, GENSTAT TWINSPAN, MULVA, MVSP, PATN, PC-ORD, PRIMER, R Package, SYN-TAX
Tabular sorting: COENOS, DECODA, MULVA, PATN, TABLCORN, PRIMER, VTAB
Ordination Polar/Bray-Curtis: Bray-Curtis, DistPCoA, PC-ORD
Ordination NMDS and PCoA, CAP: DECODA, DistPCoA, GENSTAT , MULVA, MVSP, NETMUL, PATN, PC-ORD, PRIMER, R Package, SYN-TAX
Ordination PCA: ADE-4, CANOCO, CAP, GENSTAT MULVA, MVSP, NETMUL, Parallel Analysis, PATN, PCA-H MATLAB, PC-ORD, PRIMER, R Package, SYN-TAX
Ordination RDA: CANOCO for Windows 4.0, PISCES, RdaCca, SYN-TAX
Ordination CCA: ADE-4, CANOCO for Windows 4.0, MVSP, PISCES, RdaCca, PC-ORD, SYN-TAX
Ordination CA/DCA: ADE-4, CANOCO for Windows 4.0, CAP, DECORANA, GENSTAT, MVSP, NETMUL, PATN, PC-ORD, SYN-TAX, Vista
Ordination Display: CANODRAW, ECO-LOGICA SOFTWARE, MVSP, PC-ORD, PISCES, R Package, SYN-TAX
Spatial Analysis: ADE-4,, Exeter software, GENSTAT, GS+ for Windows, Mantel Test, MRPP and Spatial Scaling Programs, MULVA, R Package, SYN-TAX
Diversity estimation and indices: EstimateS, MVSP, PC-ORD, PISCES, PRIMER, ProSoft, Rarefaction Calculator, SPECRICH
Other methods: ADE-4, BIOTA, BLOSSOM, Brodgar, CAP, Data Loom, DECODA, Exeter software, INDVAL, MEANSIM6, MRPP and Spatial Scaling Programs, MULVA, MVSP, PATN, PC-ORD, PopTools, PRIMER, Multivariate Software Inc., R Package, SYN-TAX, Vista

Informace k těmto metodám lze najít i v síti Internet, kde je možné najít i citace další důležité literatury.

Literatura

Gordon, A.D. (1973): Classification in the presence of constraints. - Biometrics, 29: 821-827.

Hájek,P.; Havránek, T.; Chytil, M.K. (1983): Metoda GUHA. – ACADEMIA Praha, 314p.

Hill,M.O. (1979): TWINSPAN - a FORTRAN program for arranging multivariate data in an ordered two way table by classification of individuals and attributes. - Ithaca(NY): Cornell Univ. 48p.

Legendre, P. (1987): Constrained clustering. In Legendre, P. & Legendre, L., Developments in Numerical Ecology - NATO ASI Ser.G, Vol. 14, pp. 289-307.

Legendre,L.; Legendre,P. [Ed.] (1983): Numerical ecology. In Developm. in environmental modelling, Vol. 3., Amsterdam 419p.

Lukasová,A.; Šarmanová, J. (1985): Metody shlukové analýzy. - SNTL Praha, 210p.

Matějka, K. (1993): Hierarchical semi-cluster analysis (HSCA): a new method of gradient analysis - Ekológia (Bratislava), 12: 131-152.

Matějka, K. (2001): Dynamika vegetace na studijních plochách v Orlických horách v letech 1951 až 2001 (zpracování dat). - Ms. [IDS Praha]

van der Maarel,E. [Ed.] (1980): Classification and ordination. In Advances in vegetation science, Vol. 2, Dordrecht: Kluwer, 188 p.

Whittaker,R.H. [Ed.] (1973): Ordination and classification of communities. In Handbook of vegetation science, Vol. 5, 738 p.

Obr. 1. Klasifikace opakovaných fytocenologických snímků bukových porostů Orlických hor podle složení bylinného patra metodou Nearest neighbour (použita Euclidovská distance jako míra nepodobnosti).

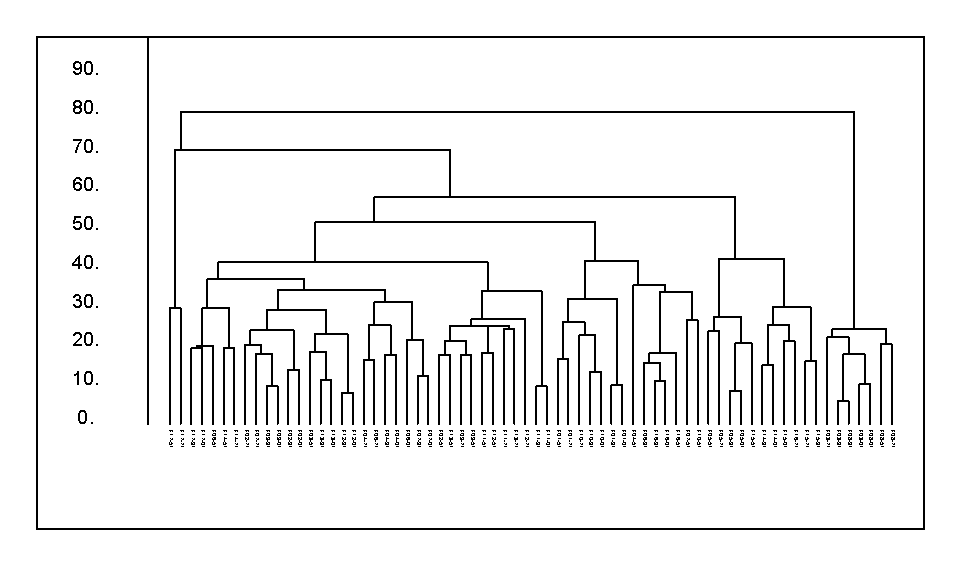
Obr. 2. Klasifikace opakovaných fytocenologických snímků bukových porostů Orlických hor podle složení bylinného patra metodou Farthest neighbour (použita Euclidovská distance jako míra nepodobnosti).

Obr. 3. Klasifikace opakovaných fytocenologických snímků bukových porostů Orlických hor podle složení bylinného patra Wardovou metodou (použit kvadrát Euclidovské distance jako míra nepodobnosti).

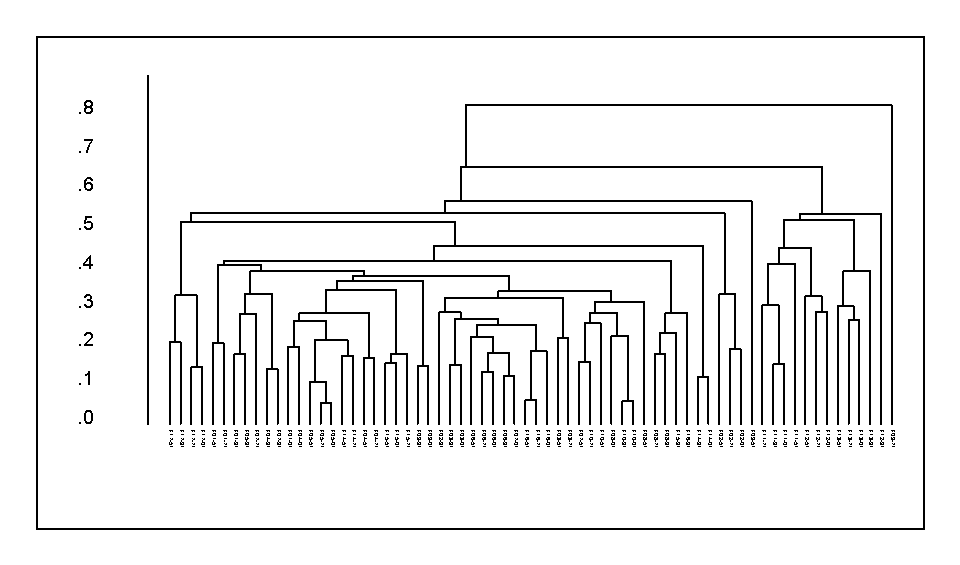
Obr. 4. Klasifikace opakovaných fytocenologických snímků bukových porostů Orlických hor podle složení bylinného patra metodou Group average (použit Sörensenův index podobnosti jako míra nepodobnosti).

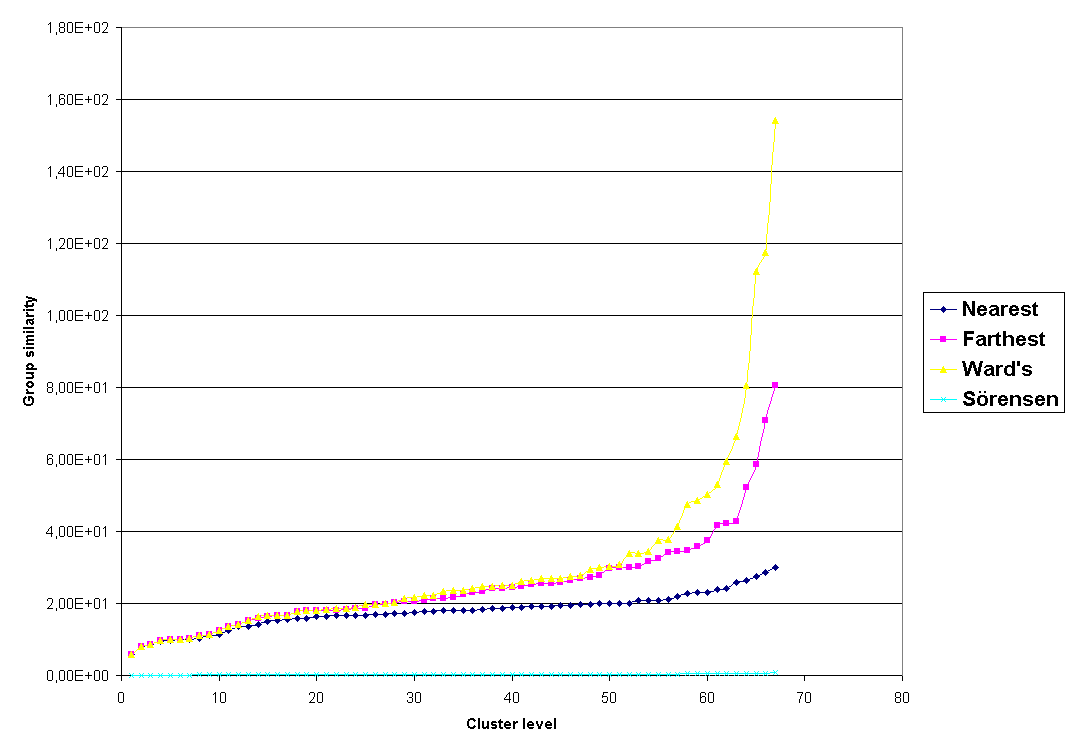
Obr. 5. Vývoj shlukování pro porovnávané klasifikační metody - hladina shlukování.

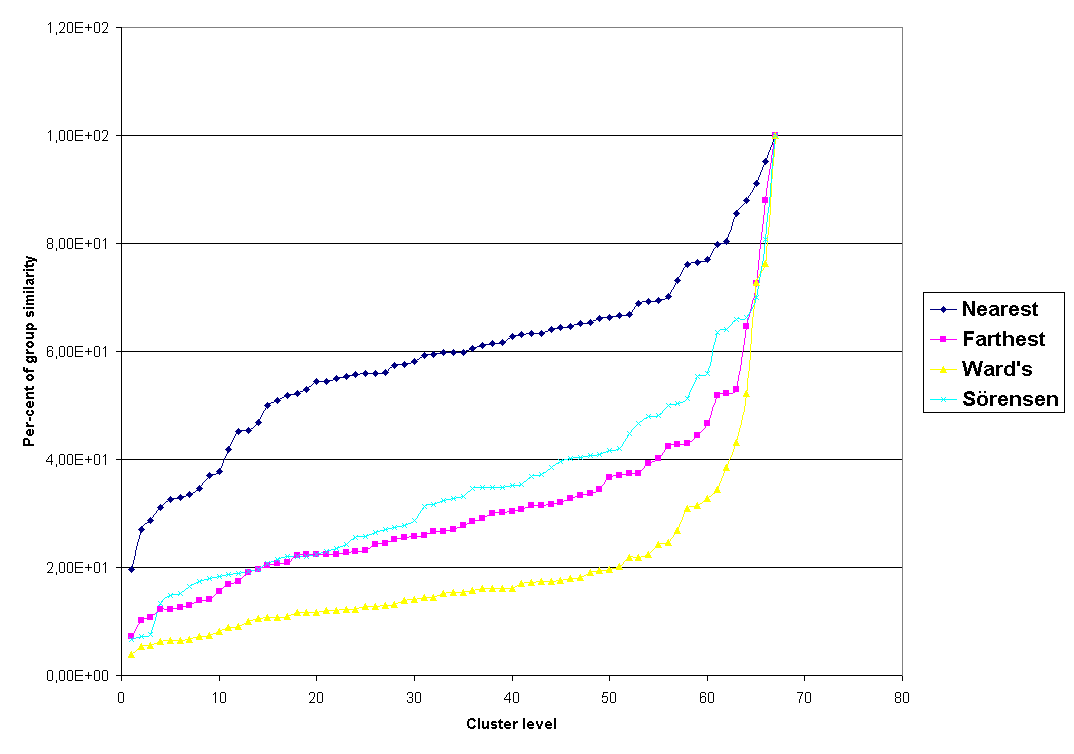
Obr. 6. Vývoj shlukování pro porovnávané klasifikační metody - podíl hladiny shlukování z celkové nepodobnosti všech vzorků.

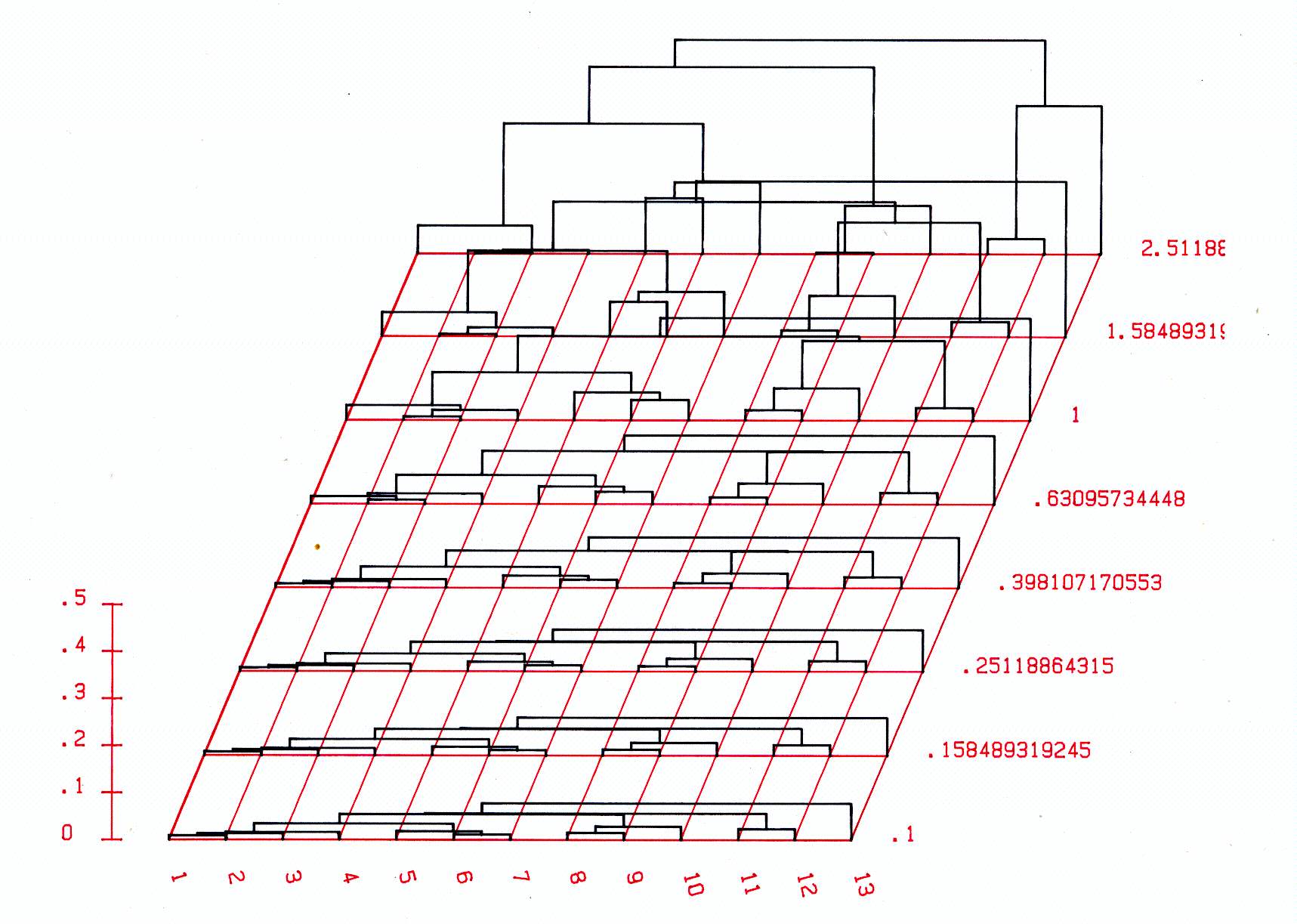
Obr. 7. Vliv mocninné transformace dat (použitá mocnina u grafu vpravo) na klasifikaci uspořádaných vzorků podél transektu bylinnou vegetací na opuštěných polích v oblasti Chelčic. Použitá metoda HSCA s indexem podobnosti Sq (Matějka, 1993).

Obr. 8. Dvě různé možnosti (A, B) klasifikace uspořádaných vzorků rozmístěných na gradientu se dvěma ekotony.

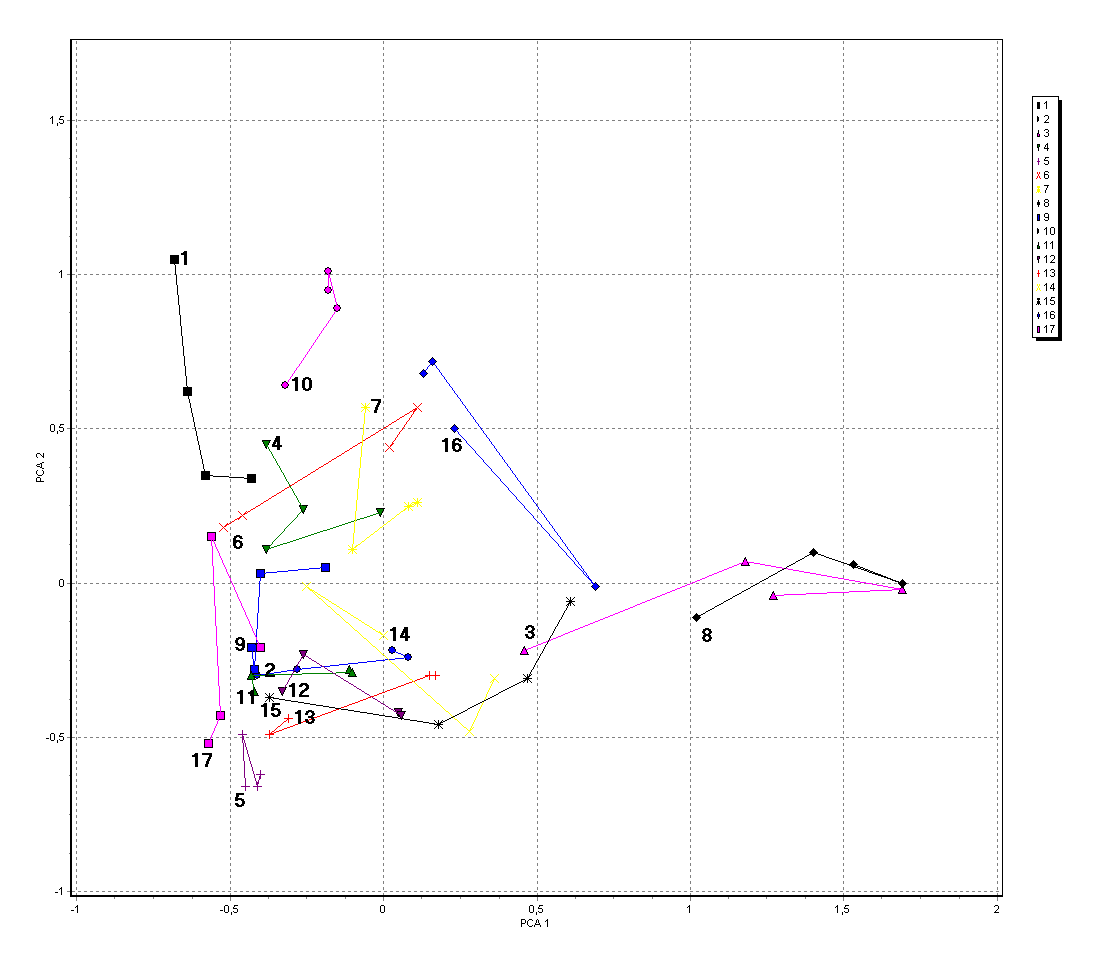
Obr. 9. Ordinace opakovaných fytocenologických snímků bukových porostů Orlických hor podle složení bylinného patra metodou PCA - zobrazeny prvé dvě osy.

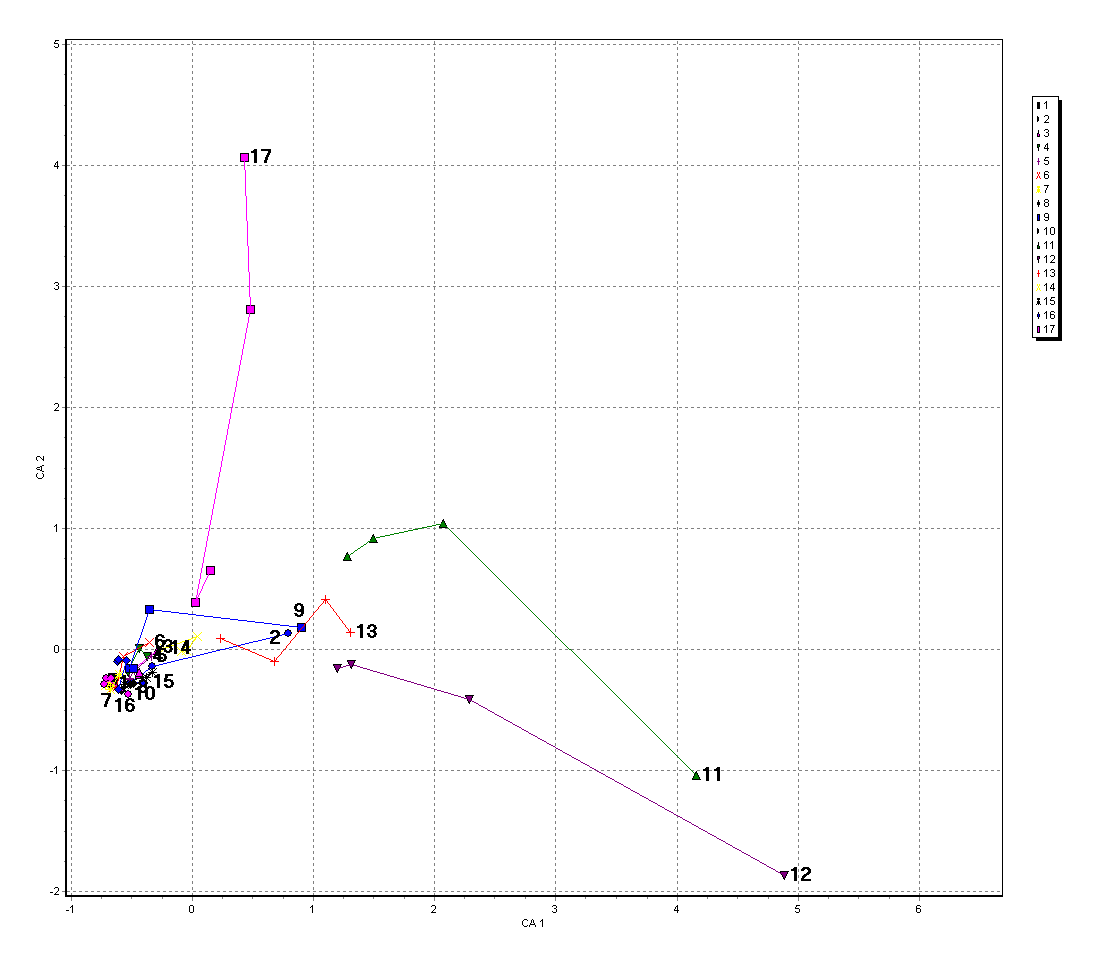
Obr. 10. Ordinace opakovaných fytocenologických snímků bukových porostů Orlických hor podle složení bylinného patra metodou CA - zobrazeny prvé dvě osy.

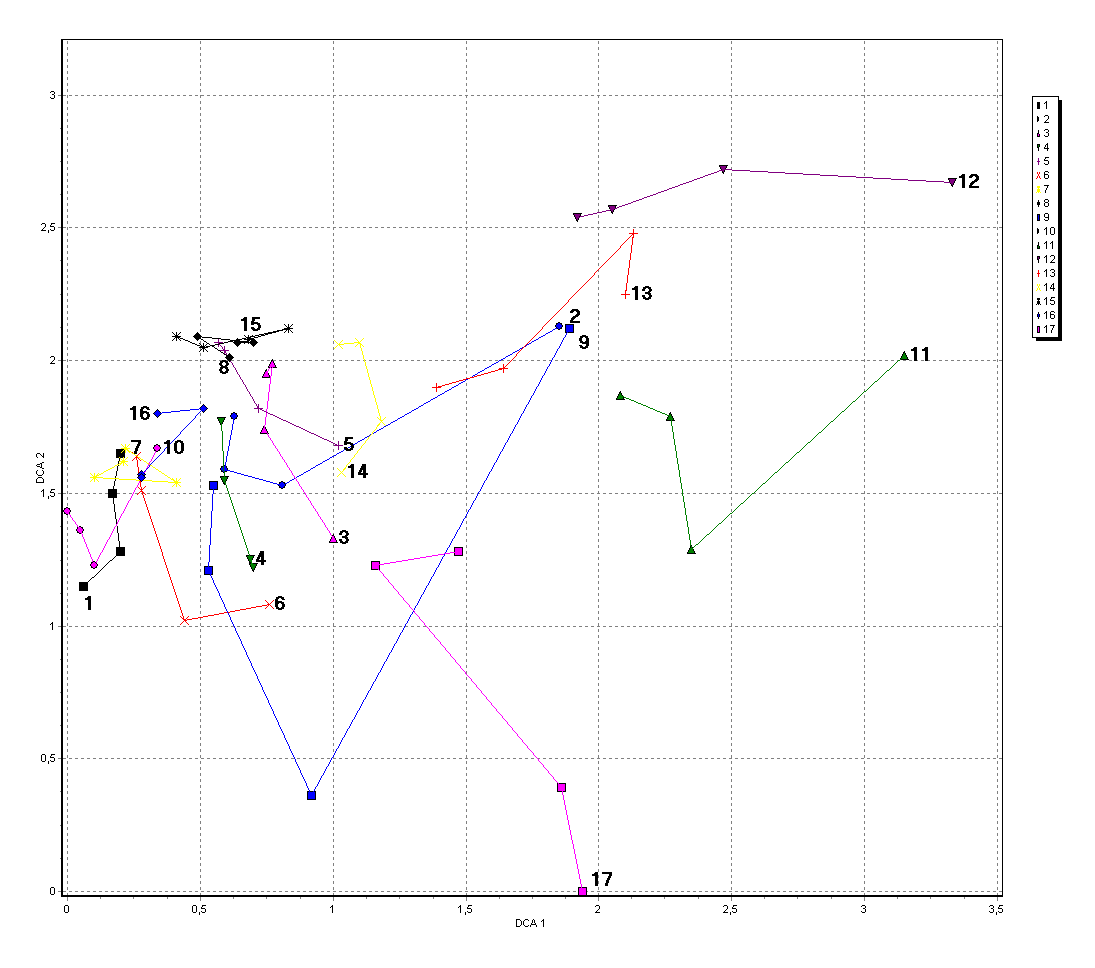
Obr. 11. Ordinace opakovaných fytocenologických snímků bukových porostů Orlických hor podle složení bylinného patra metodou DCA (detrending by segments) - zobrazeny prvé dvě osy.

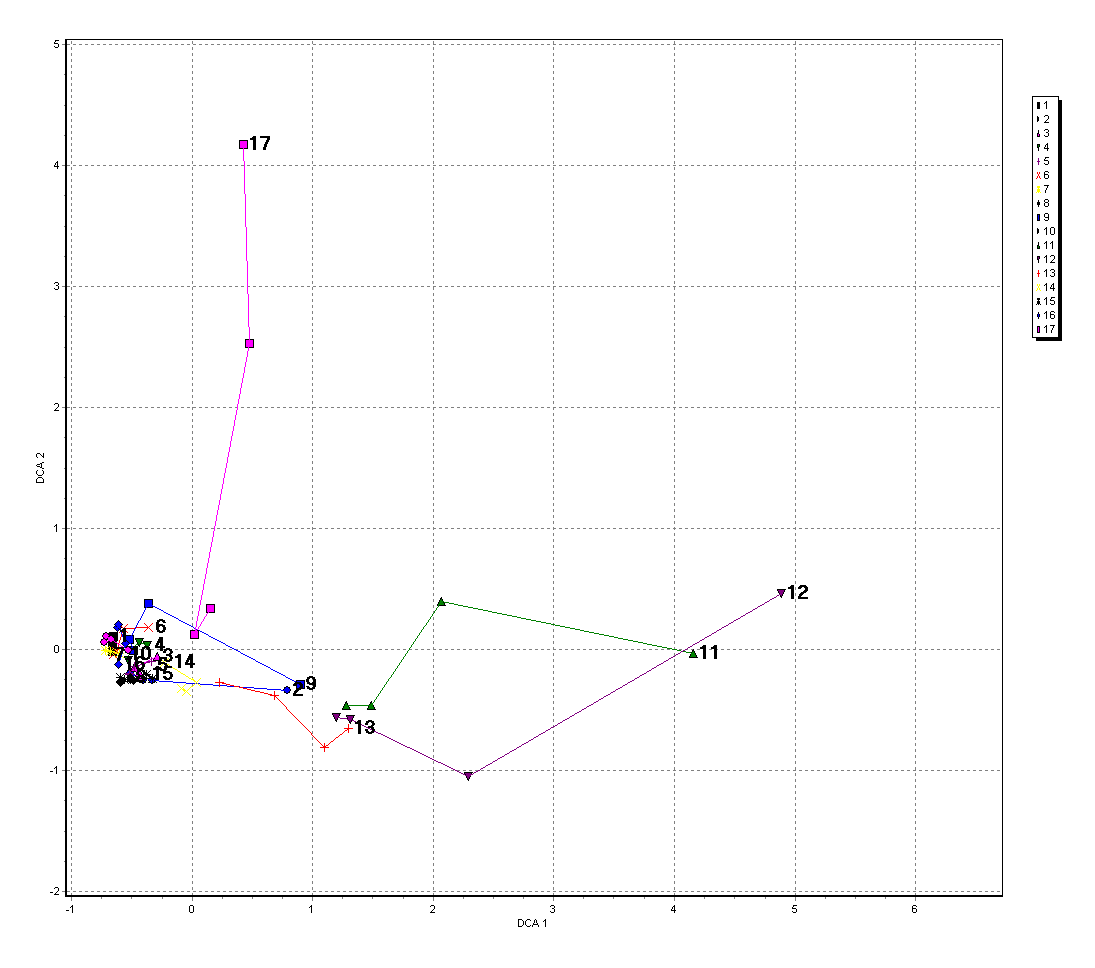
Obr. 12. Ordinace opakovaných fytocenologických snímků bukových porostů Orlických hor podle složení bylinného patra metodou DCA (detrending by 2nd order polynomials) - zobrazeny prvé dvě osy.

Obr. 13. Ordinace druhů z opakovaných fytocenologických snímků bukových porostů Orlických hor, metoda DCA (detrending by 2nd order polynomials) - zobrazeny prvé dvě osy.

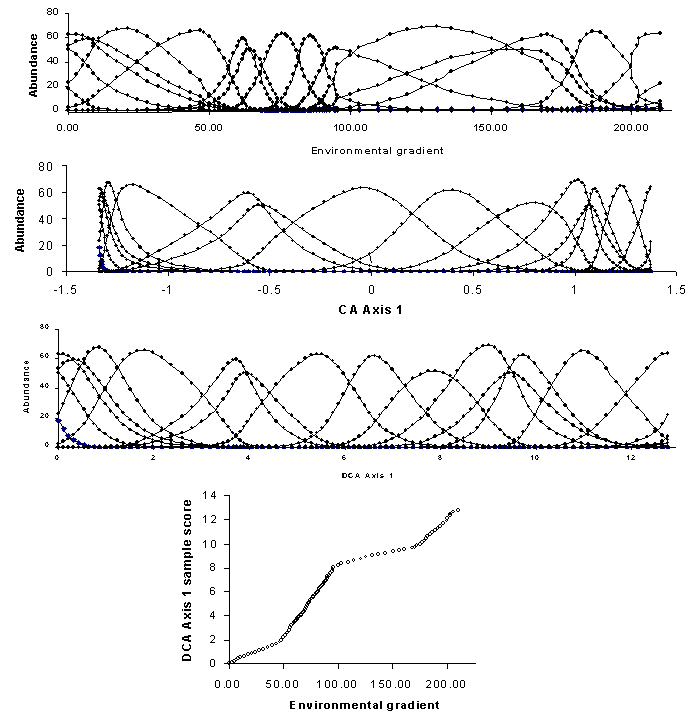
Obr. 14. Znázornění rozdělení výskytu (abundance) druhů podél environmentálního gradientu a znázornění tohoto gradientu na základě ordinační metody CA a DCA.

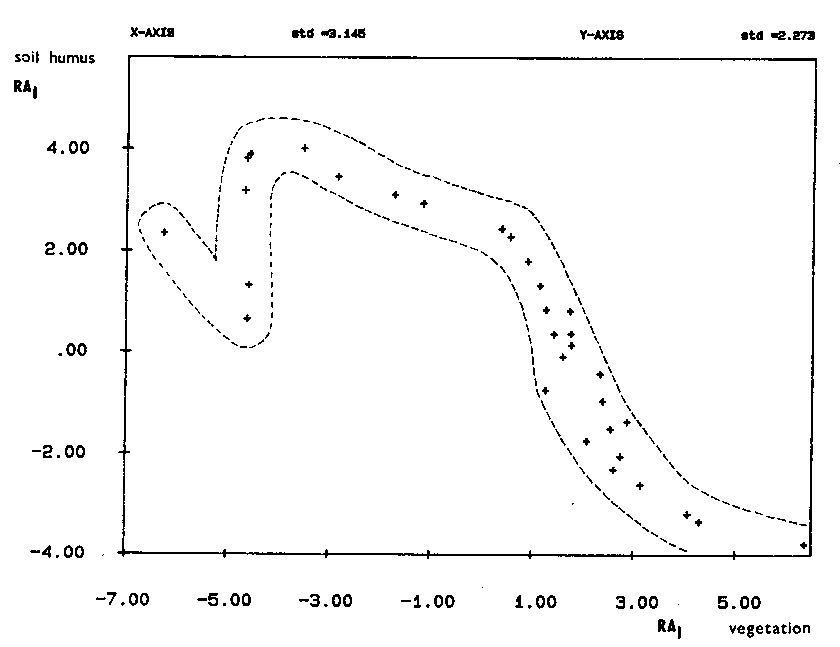
Obr. 15. Porovnání prvých ordinačních os dat vegetace a dat o složení humusu v půdě podél transektu luční vegetací. Použita metoda CA pro obě datové sady.

Zpět na hlavní stránku IDS